Damit ein Fahrzeug autonom fahren kann, sind einige Kernfunktionalitäten mit entsprechender Algorithmik notwendig: Die Bestimmung der aktuellen Position und Ausrichtung, das Berechnen eines Weges vom gegenwärtigen Ort zu einem Zielpunkt, das Verfolgen dieses Weges zum Ziel, der Umgang mit unerwarteten Hindernissen und natürlich die entsprechende Ansteuerung und Regelung der Motoren und der Lenkung.

Standortbestimmung eines autonomen Systems

Es ist klar, dass die Ermittlung der eigenen Position von primärer Bedeutung ist. In vielen Anwendungen reicht ein einzelner Positionssensor (zum Beispiel ein GPS-Empfänger im Freien oder UWB in Räumen) alleine nicht aus, um eine befriedigende, genügend dynamische und präzise Positionsschätzung zu erhalten. Statt dessen werden weitere Grössen gemessen und benutzt, zum Beispiel die Geschwindigkeit und Beschleunigung des Fahrzeugs, die Himmelsrichtung und deren Änderung, usw. Mittels Sensor Fusion (zum Beispiel durch ein Kalman Filter) wird daraus eine gemeinsame Schätzung erzeugt.

Schwächen einzelner Sensoren mit Algorithmik verbessern

Zudem wird voraus gesetzt, dass ein autonomes System in der Lage ist, Hindernisse in der Umgebung zu erfassen, um darauf entsprechend zu reagieren, zum Beispiel indem das autonome Fahrzeug stoppt oder ihnen ausweicht. Bei solchen Anti-Kollisionssystemen will man sich im Normalfall auch nicht auf einen einzelnen Sensor verlassen.

Die Schwächen und Stärken der einzelnen Sensoren 

Ein Ultraschallsystem ist nicht geeignet für lange Distanzen; Radar kann sehr kleine Hindernisse, etwa einen Maschendraht, übersehen; ein Laserdistanzmesssystem (Lidar) schwächelt bei Regen und ein optisches System mit Kameras kann bei Nebel oder direkter Sonneneinstrahlung keine guten Resultate erzielen. Die Schwächen und Stärken der einzelnen Sensoren können durch geeignete Algorithmik zu einem robusten und zuverlässigen Gesamtsystem vereint werden.

Autonome System findet Weg mit Path Planner

Eine weitere wichtige Grundfunktion eines autonomen Systems ist natürlich das Anfahren eines Ziels. Für die meisten industriellen Anwendungen genügt es nicht, dass das autonome Fahrzeug sich in Richtung des Zielpunktes bewegt und unterwegs Hindernissen ausweicht. Statt dieser eher zufälligen Strategie ist es oft erwünscht, von der eigenen Position zum Ziel, unter Berücksichtigung von bekannten Hindernissen, den (oder einen) optimalen Weg zu finden. Der sogenannten Path Planner ist dafür verantwortlich.

Der elementare Path Planner

Die Aufgabe des Path Planners besteht also darin, für das autonome System von einem Startpunkt aus einen optimalen Weg zum Ziel zu berechnen. Was optimal ist, definiert ein bestimmtes Kriterium, zum Beispiel indem der Weg minimale Steigungen haben soll, minimalen Treibstoffverbrauch verursacht, keine zu engen Kurven enthält oder etwas Ähnliches.

Wenn der kürzeste Weg gesucht wird

Oft jedoch ist einfach der kürzeste Weg gesucht. Bekannte Hindernisse werden in einer Karte markiert und dem Algorithmus zur Verfügung gestellt. Zur Illustration stelle man sich eine Lagerhalle vor, in der sich ein autonomer Roboter bewegt. Der soll nun auf dem kürzesten Weg zu einer gewissen Stelle bei Regal C fahren. Eine entsprechende Karte ist in Abbildung 2 dargestellt. Beachte, dass die Regale Hindernisse darstellen.

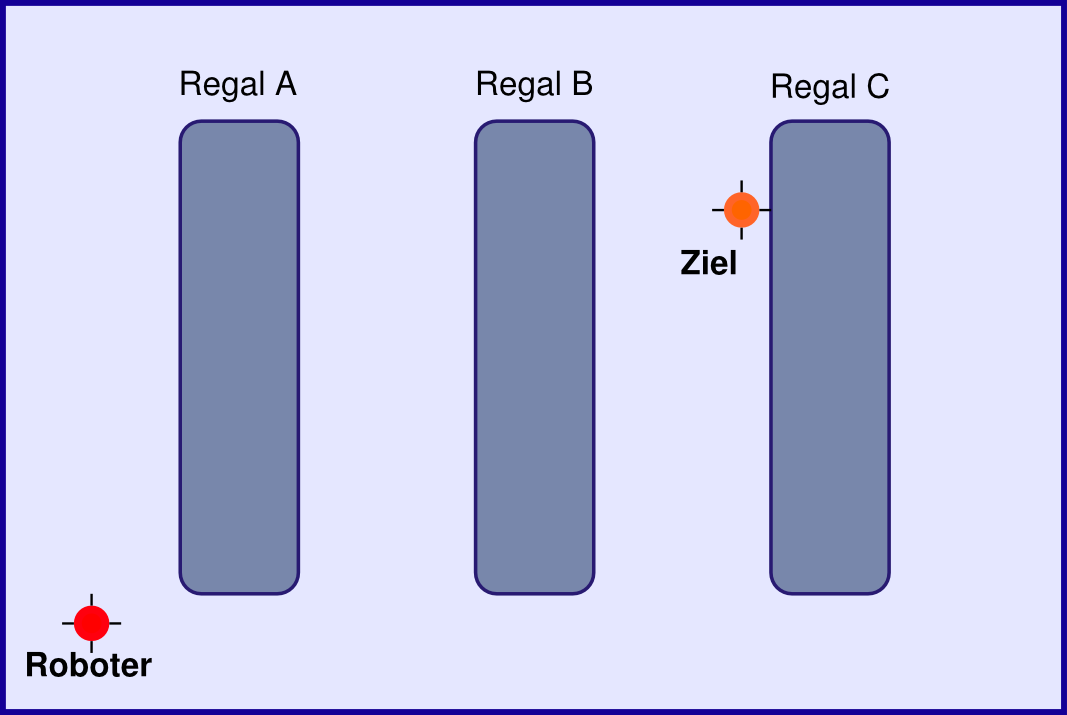
Eine Strategie: die diskretisierte Karte

Eine Strategie, um dieses Problem zu lösen, geht von einer diskretisierten Karte aus (siehe Abbildung 3). Dabei wird ein Gitter mit Zellen über die Karte gelegt. Dann wird eine Bewertungsfunktion definiert. Mit Hilfe dieser Funktion wird anschliessend für jede Zelle iterativ eine Art Kostenwert errechnet. Jede Kostenzahlen wird direkt in die jeweils betreffende Zelle notiert.

Einfache Annäherung an die Euklidische Distanz

Wenn wir den kürzesten Weg vom Startpunkt zum Ziel finden wollen, so wählen wir als Kosten eines Feldes sinnvollerweise gerade die Anzahl Felder, die überquert werden müssen, um vom Startpunkt zum Feld zu gelangen. Die Distanz zwischen zwei horizontal oder vertikal benachbarten Feldern zählen wir als eine Einheit. Bei diagonal benachbarten Feldern zählen wir die Distanz als 1.4 Einheiten, was eine einfache Annäherung an die Euklidische Distanz ist (die Quadratwurzel aus zwei).

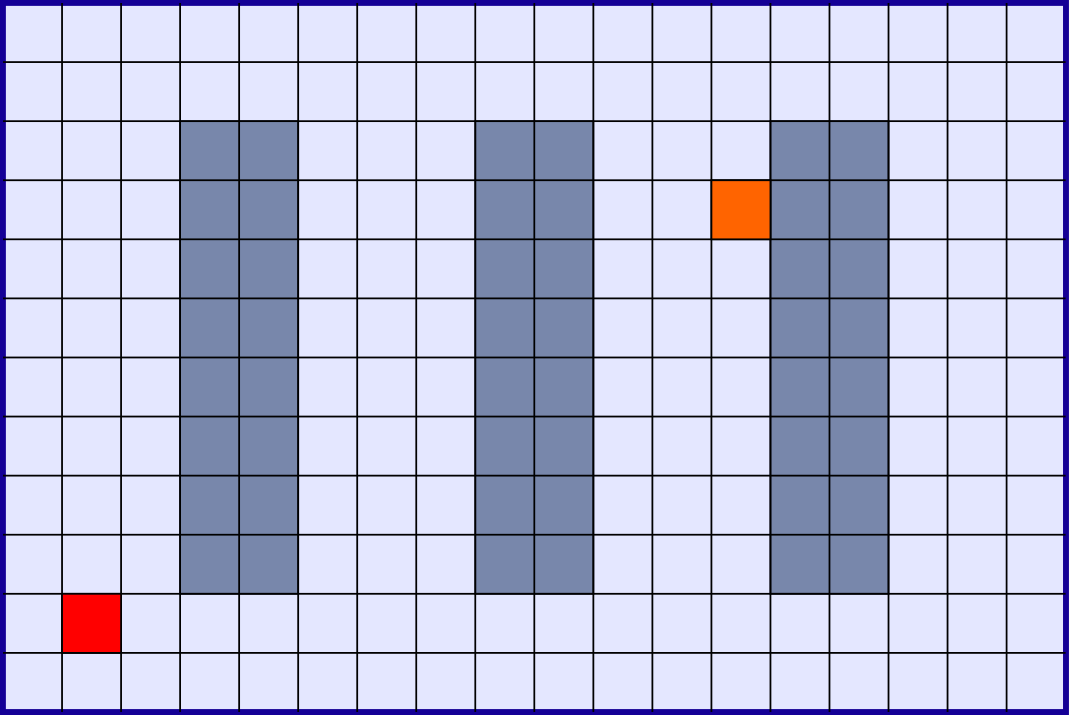
Vorgehen zur Berechnung der Kostenfunktion

Um für alle Zellen, über welche das autonome System fahren wird, bis zum Ziel die Kostenfunktion zu berechnen, geht man so vor:

1. Es werden alle befahrbaren Zellen auf den Kostenwert unendlich.
2. Alle befahrbaren Zellen werden als noch nicht besucht markiert (weiss).
3. Die Startzelle erhält den Kostenwert 0.

Iterativ werden nun die Kosten der Knotenpunkte nach folgendem Schema reduziert:

4. Wähle unter den vom autonomen System noch nicht besuchten Zellen jene mit dem tiefsten Kostenwert aus und markiere sie temporär (gelb). Sollte es mehrere Kandidaten mit dem selben tiefsten Kostenwert geben, so wähle einen davon aus.
5. Berechne die Kostenfunktion für alle unmittelbaren Nachbarzellen, die noch nicht besucht wurden (temporär grün).
6. Vergleiche für jeden Nachbarn den betreffenden neuen Kostenwert mit dem schon bestehenden und übernimm den tieferen Wert von beiden.
7. Markiere die aktuelle Zelle als besucht (blau).
8. Wiederhole die Punkte 4 bis 7 solange, bis die Zielzelle als besucht markiert wurde.

Nun kann der kürzeste Weg ausgelesen werden:

9. Wähle als Ausgangspunkt die Zelle am Ziel.
10. Wähle unter den unmittelbaren Nachbarzellen, die als besucht markiert sind, jene Zelle als Nachfolger im Pfad aus, die den kleinsten Kostenwert hat. Markiere sie (roter Rand). Sollte es mehrere Kandidaten mit dem selben tiefsten Kostenwert geben, so wähle einen davon aus.
11. Wiederhole Punkt 10 für jede Nachfolgerzelle so lange, bis der Startpunkt erreicht ist.

Abbildungen 4 bis 12: So sieht das Verfahren auf Karten aus

Der eben beschriebene Algorithmus ist übrigens nicht neu. Er wurde von Edsger Dijkstra 1959 publiziert, als von autonomen Systemen und Fahrzeugen noch kaum die Rede war, und ist heute Teil der modernen Graphen-Theorie.

In den Abbildungen 4 bis 12 wird das Verfahren auf unsere Beispielkarte angewendet.

Abbildung 4 zeigt die initialisierte Karte. Der Startpunkt ist als ausgewählt markiert (gelb). Die Kostenwerte seiner  Nachbarn (grün) werden in der ersten Iteration reduziert.

In Abbildung 5 sind die neuen Kostenwerte eingetragen. Damit ist die erste Iteration abgeschlossen, die Startzelle wird als besucht markiert (blau). Jetzt wird die nächste Zelle ausgewählt, nämlich eine, die noch nicht besucht ist und davon jene, die aktuell den kleinsten Kostenwert hat.

Abbildung 6 zeigt, dass das Feld links des Startpunktes gewählt wurde. Es hätte noch drei weitere Kandidaten mit dem selben Kostenwert gegeben. Die Wahl ist zufällig. Wiederum bezeichnen die grünen Felder jene, die in der zweiten Iteration aufdatiert wurden.

Abbildung 7 zeigt den Zustand nach der dritten Iteration.

Die folgenden Abbildungen 8 und 9 zeigen, wie die blaue Fläche der schon besuchten Felder sich langsam in alle Richtungen ausbreitet.

In Abbildung 10 wird die Zielzelle erreicht und in Abbildung 11 wird das Ziel als besucht markiert. Damit endet der Algorithmus.

In Abbildung 12 ist der gesuchte Weg markiert. Er  folgt rückwärts vom Ziel zum Start, entlang des grössten Gradienten.

Verbesserungen - denn Dijkstras Algorithmus hat ein Problem

Obwohl das wunderbar funktioniert, hat Dijkstras Algorithmus ein Problem: Je nach Auflösung und Grösse der Karte kann das Verfahren eine extrem hohe Anzahl von Iterationen erfordern und ist folglich für Echtzeitsysteme schlecht geeignet. Aus diesem Grund gibt es einige Varianten davon.

Das A*Verfahren verbessert die Effizienz

Das sogenannte A*Verfahren verbessert in erster Linie die Effizienz. Zu diesem Zweck wird die Kostenfunktion (Entfernung eines Feldes vom Startpunkt) erweitert durch eine heuristische Schätzung der Distanz des Feldes zum Ziel. Die beiden Entfernungen werden addiert. Das führt dazu, dass der Kostenwert von Zellen, die vom Ziel weg führen, anwachsen und folglich nicht sofort weiter verfolgt werden. Erst wenn die scheinbar direkten Wege nicht zum Ziel führen, greift der Algorithmus auf diese Zellen zurück.

Der D*Algorithmus umgeht das Problem des sich verändernden Startpunktes

Der D*Algorithmus ist für autonome Systeme besonders nützlich. Er beginnt nicht beim Startpunkt und sucht den kürzesten Weg zum Ziel, sondern umgekehrt: Er sucht den kürzesten Weg vom Ziel zum Startpunkt. Dabei verwendet er im Wesenlichen das A*Verfahren. Verändert sich nun der Startpunkt, weil sich das autonome System bewegt und tritt plötzlich ein zuvor noch nicht bekanntes Hindernis auf, so muss nicht der gesamte Weg neu berechnet werden. Statt dessen wird die Kostenkarte nur partiell in der Umgebung des Hindernisses aufdatiert. Vom Hindernis zum Ziel bleiben die Kostenwerte erhalten. Dies erlaubt ein schnelles Umplanen und Reagieren auf unvorhergesehene Veränderungen der Karte.

Fazit

Das Fazit zu Path Planning bei autonomen Systemen

Path Planning ist bei autonomen Systemen nicht wegzudenken und bildet einen essentiellen Bestandteil intelligenter Fahrzeuge. Gerade im Vergleich zu autonomen Systemen ohne diese Fähigkeit, welche oft den Anschein erwecken, als irren sie ziellos umher, wird schnell klar, wie wichtig ein solches Verfahren in der Praxis ist.

Der Rechenaufwand ist indessen nicht zu vernachlässigen. Ausserdem muss der Path Planner mit unerwarteten Hindernissen oder Änderungen der Karte zurecht kommen. Verschiedene Varianten des klassischen Dijkstra-Algorithmus tragen diesen Bedürfnissen Rechnung.