Die Krux mit der Totzeit

Will man ein System regeln, das mit Totzeit behaftet ist, das also stets verspätet reagiert, so kann das Leben sehr frustrierend sein. Standard PID-Regler versagen oder müssen derart passiv eingestellt werden, dass am Ende von Prozess-Dynamik keine Rede mehr sein kann. Ein Smith-Prädiktor entschärft das Problem erheblich.

Otto Smith war ein typischer Erfinder. 1917 in Illinois, USA, geboren, studierte er Elektrotechnik, doktorierte und arbeitete anschliessend in diversen Firmen und Forschungsanstalten. Ab 1947 bis zu seiner Pensionierung 1988 war er Professor an der Universität von Berkeley. Er war somit aktiv in der Periode der grossen Entdeckungen in der Elektrotechnik und zählt heute zu den wichtigsten Persönlichkeiten jener Zeit. Er meldete gegen 50 Patente an und veröffentlichte weit über 100 Publikationen unter anderem im Bereich der netzseitigen Ansteuerung und Regelung von Elektromotoren. In diesem Zusammenhang stiess er auf das Problem der Totzeit.

Falsche Wertbildung

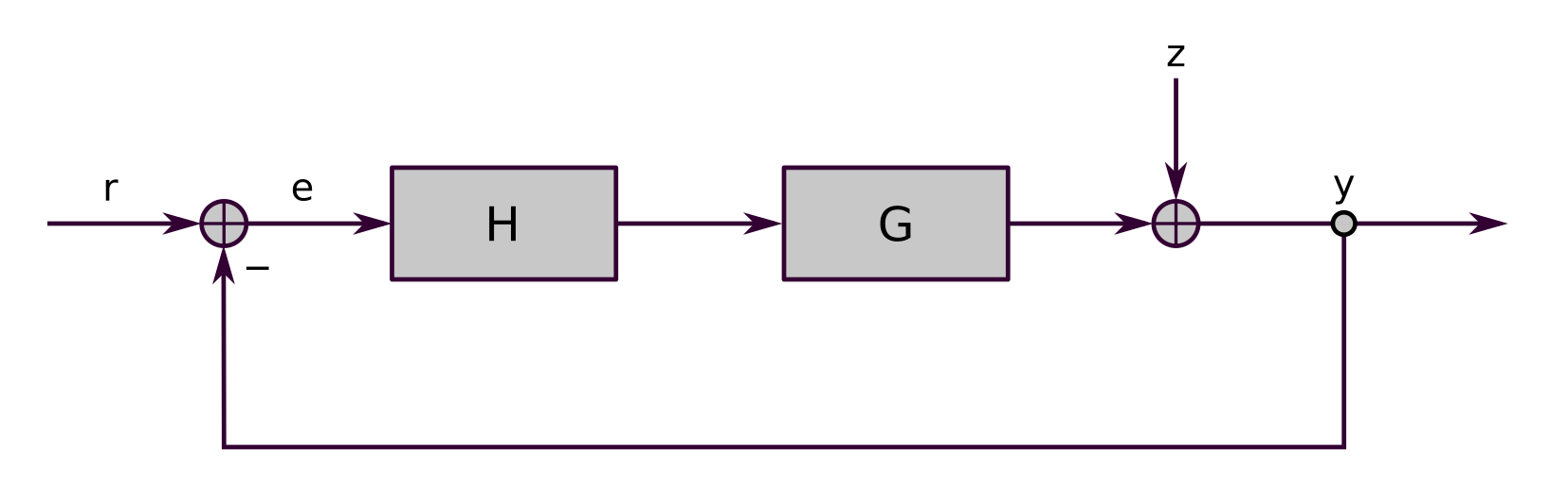
Ein klassischer Regelkreis ist in Abbildung 1 dargestellt. Der Regler H treibt den Prozess, resp. die Strecke oder das System G an. Am Ausgang der Strecke G wirkt die Störgrösse z, so dass sich der Ausgang y des Systems oft nicht exakt so verhält, wie es der Sollwert r verlangt. Aus diesem Grund wird aus Soll- und Istwert der Regelfehler e = r-y berechnet, den der Regler zu null machen soll.

Beinhaltet G nun eine Totzeit, wie das typischerweise bei thermischen Prozessen, bei Transport- und Abfüllanlagen, aber auch bei vielen Antriebsanwendungen mit Spiel oder Elastizität und Reibung der Fall ist, so reagiert die Strecke G immer verzögert.

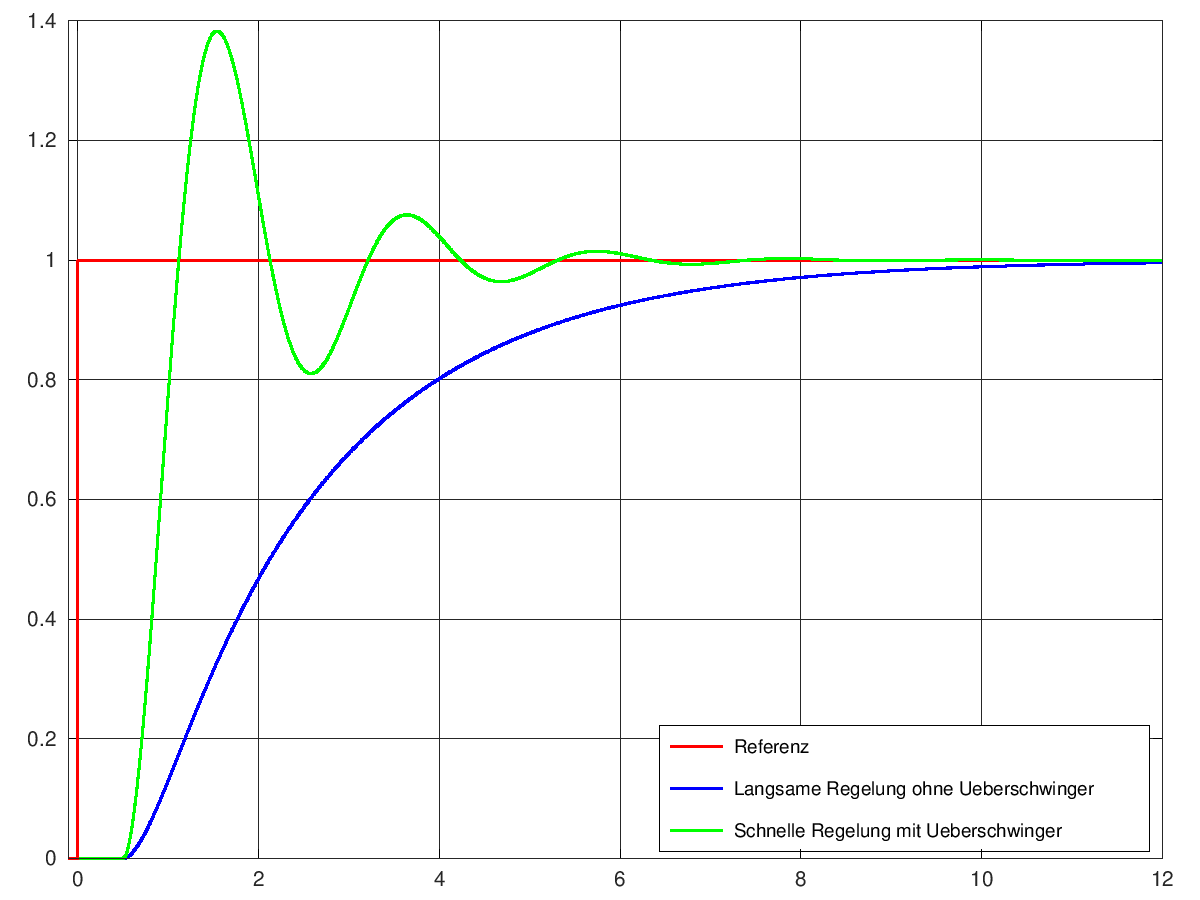
Das heisst, dass der Fehler e aus Werten gebildet wird, die zeitlich gar nicht zusammen gehören. Oder anders ausgedrückt: Der Regler versucht immer einen Fehler auszuregeln, den er noch gar nicht kennt, weil er erst später auftritt. Dadurch neigt das Gesamtsystem zu Instabilität, was bedeutet, dass der Regler sehr schwach eingestellt werden muss, was wiederum dazu führt, dass der Prozess nur langsam reagiert. Das ist in Abbildung 2 dargestellt.

PID-Regler oder wie man einen geeigneten Regler für eine Strecke mit Totzeit findet

Oft ist H ein PID-Regler. Die Vorteile davon sind primär, dass dessen Verhalten leicht verständlich und nachvollziehbar ist, dass es für gutmütige Strecken einfache Einstellregeln gibt und dass seine (beschränkten) Fähigkeiten für moderate Anforderungen oft ausreichen. Mit Totzeit sieht das etwas anders aus und es gilt folgende Faustregel für PID-Regler. Dabei ist T die Totzeit und S die Zeitkonstante des Systems:

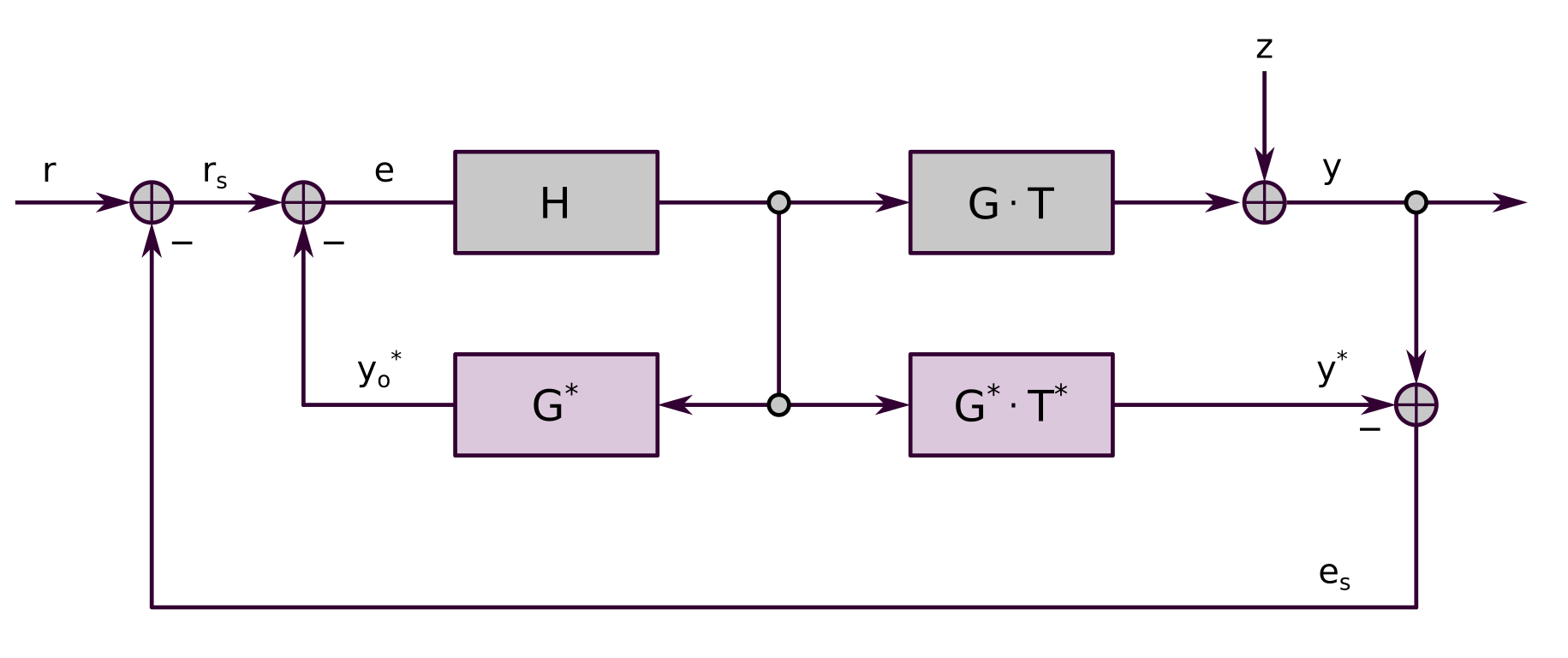
Versucht man einen geeigneten Regler für eine Strecke mit Totzeit zu finden, so stellt man bald fest, dass der Regler die Fähigkeit haben müsste, in die Zukunft zu sehen. Das ist natürlich nicht möglich, aber mit Hilfe eines Modells kann man das zukünftige Verhalten eines Systems mindestens im Voraus schätzen. Der Smith-Prädiktor tut genau das. Das Blockschaltbild eines Reglers mit Smith-Prädiktor ist in der Abbildung 3 dargestellt. H bezeichnet wiederum den Regler, zum Beispiel einen PID-Regler. G·T ist das Verhalten der Strecke, wobei wir jetzt davon ausgehen, dass sich die Totzeit T und das reine Verhalten der Strecke G ohne Totzeit separieren lassen. Das ist der Kern von Smiths Idee.

Modell, um Totzeit zu umgehen

Für die Realisierung des Reglers verwendet Smith nun mathematische Modelle für G und T. Um anzuzeigen, dass es sich um Modelle handelt, sind sie in Abbildung 3 mit G^*, resp. T^* bezeichnet. Die Modelle findet man durch eine Systemidentifikation und entsprechende Übertragungsfunktionen. Mit diesen Modellen lässt sich die Totzeit jetzt umgehen, denn mit H und G^* lässt sich ein Regelkreis ohne Totzeit bilden (linke Hälfte von Abbildung 3). Der Regler H für diesen Kreis lässt sich demnach leicht nach den üblichen Regeln einstellen. Wir simulieren an dieser Stelle also den ursprünglichen Regelkreis aber ohne die Totzeit. Folglich ist y₀^* eine Vorhersage des wahren Streckenausgangs y.

Modellbasierte Regelung mit Smith-Prädiktor robust gegenüber Modellfehlern

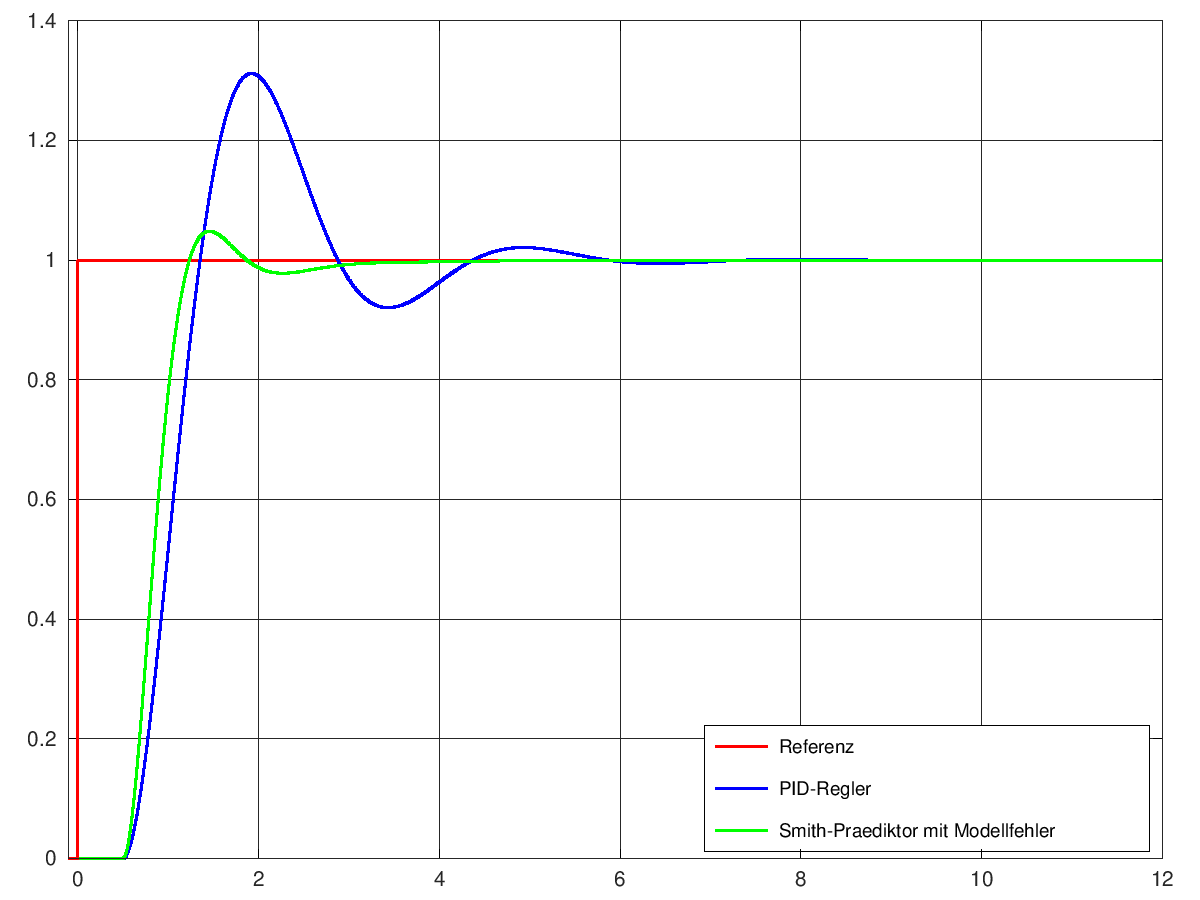
Da das Modell G^* und die geschätzte Totzeit T^* in der Regel nicht perfekt sind, wird mit Hilfe von  H und G^*·T^* auch noch eine Schätzung von y gemacht. Wir nennen sie y^*. Mit y-y^* erhält man schliesslich den verbleibenden Regelfehler, der auf Grund des Modellfehlers und der Störgrösse z resultiert (rechte Seite von Abbildung 3). Dieser Restfehler wird ebenfalls auf den Regler H zurück geführt. Es zeigt sich (siehe Abbildung 4), dass mit dieser Topologie deutlich bessere Resultate erzielt werden, als mit dem einfachen PID-Regler gemäss Abbildung 1. Die modellbasierte Regelung mit Smith-Prädiktor ist ziemlich robust gegenüber Modellfehlern. Dennoch gilt natürlich: Je bessser das Modell, desto besser die Regelgüte. Darin liegt auch die Herausforderung bei der Realisierung.

Otto Smith hat uns mit seinem Regleransatz ein nützliches Werkzeug für den Umgang mit reiner Totzeit hinterlassen. Seine Idee wurde in neuerer Zeit in vielfäliger Weise weiter entwickelt, so dass inzwischen viele schwierige Fälle, auch solche, die von Natur aus instabil sind, handhabbar geworden sind. Stettbacher Signal Processing AG ist seit über 20 Jahren auf dem Gebiet der Signalverarbeitung und Regelungstechnik tätig und ist kompetenter Entwicklungspartner, wenn es um die Modellierung physikalischer Vorgänge, die Entwicklung von Modellen und die Lösung von regelungstechnischen Problemen geht. Die Firma bietet zu diesen Themen auch Kurse an, bei denen die Grundlagen theoretisch aufgearbeitet und anhand von praktischen Übungen vertieft werden.